1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
// polygon vertices sort by angle
// @mango
#include "opencv2/opencv.hpp"
//base on opencv
int main()
{
//顺时针 {12.0, 3.0} { 12.0, 20.0} {0.0, 13.0} {-11.0, 12.0} {-12.0, 0。0} {-11.0, -12.0} {0.0, -15.0}
std::vector<cv::Point2f> polygon;
polygon.push_back({ 12.0f, 20.0f });
polygon.push_back({ 12.0f, 3.0f });
polygon.push_back({ -11.0f, 12.0f });
polygon.push_back({ 0.0f, 13.0f });
polygon.push_back({ 0.0f, -15.0f });
polygon.push_back({ -11.0f, -12.0f });
polygon.push_back({ -12.0f, 0.0f });
//step1
cv::Point2f centroid = { 0.0f, 0.0f };
for (const auto& pt : polygon)
{
centroid.x += pt.x;
centroid.y += pt.y;
}
auto count = polygon.size();
centroid.x = centroid.x / count;
centroid.y = centroid.y / count;
auto cmp_angle = [&](cv::Point2f& a, cv::Point2f& b)
{
//step2
//将转换坐标系写进匿名函数
auto a_offset = a - centroid;
auto b_offset = b - centroid;
//按角度升序排序(顺时针),若需要逆时针将小于号改为大于号即可
//opencv图像坐标系为如下图,角度升序对应顺时针
//(0,0)----------------------x+-------->
// .
// .
// y+
// .
// V
//step3
return cv::fastAtan2(a_offset.y, a_offset.x) < cv::fastAtan2(b_offset.y, b_offset.x);
};
std::sort(polygon.begin(), polygon.end(), cmp_angle);
for (auto& pt : polygon)
{
std::cout << pt << std::endl;
}
return 0;
}
|
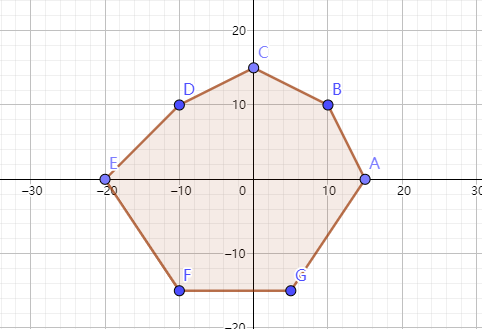 现有一组凸多边形二维平面坐标数组
现有一组凸多边形二维平面坐标数组