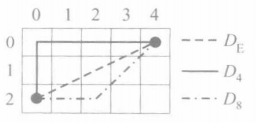
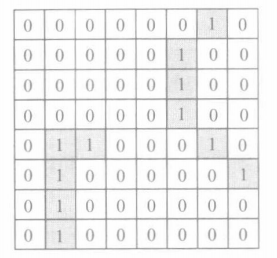
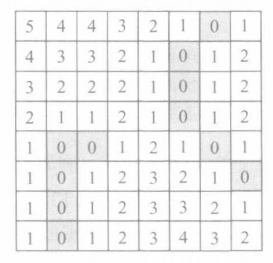
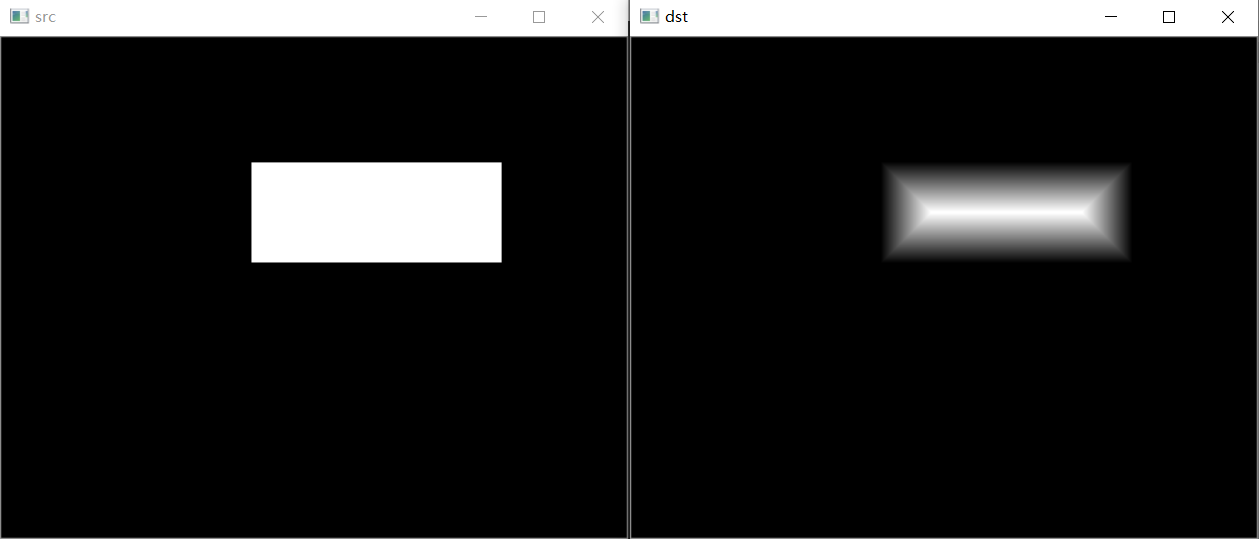
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
|
// Copyright https://mangoroom.cn
// License(MIT)
// Author:mango
// distance transfer | 距离变换
// this is distance_transform.cpp
#include"distance_transfer.h"
#include<array>
void imageprocess::DistanceTransform(const cv::Mat& src_image, cv::Mat& dst_image)
{
//step1: check the input parameters: 检查输入参数
assert(!src_image.empty());
assert(src_image.channels() == 1);
//step2: initialize dst_image : 初始化目标图像
cv::threshold(src_image, dst_image, 100, 255, cv::THRESH_BINARY);
//step3: pass throuth from top to bottom, left to right: 从上到下,从做到右遍历
for (size_t i = 1; i < dst_image.rows - 1; i++)
{
for (size_t j = 1; j < dst_image.cols; j++)
{
//AL AL
//AL P
//AL
std::array<cv::Point, 4> AL;
AL.at(0) = cv::Point( i - 1, j - 1 );
AL.at(1) = cv::Point( i - 1, j );
AL.at(2) = cv::Point( i, j - 1 );
AL.at(3) = cv::Point(i + 1, j - 1 );
int Fp = dst_image.at<uchar>(i, j);
//Fq
std::array<int, 4> Fq = { 0 };
Fq.at(0) = dst_image.at<uchar>(i - 1, j - 1);
Fq.at(1) = dst_image.at<uchar>(i - 1, j);
Fq.at(2) = dst_image.at<uchar>(i, j - 1);
Fq.at(3) = dst_image.at<uchar>(i + 1, j - 1);
std::array<int, 4> Dpq = { 0 };
std::array<int, 4> DpqAddFq = { 0 };
for (size_t k = 0; k < 4; k++)
{
//D(p, q)
Dpq.at(k) = D4(i, AL.at(k).x, j, AL.at(k).y);
//D(p,q) + F(q)
DpqAddFq.at(k) = Dpq.at(k) + Fq.at(k);
}
//F(p) = min[F(p), D(p,q) + F(q)]
std::sort(DpqAddFq.begin(), DpqAddFq.end());
auto min = DpqAddFq.at(0);
Fp = std::min(Fp, min);
dst_image.at<uchar>(i, j) = Fp;
}
}
//step4: pass throuth from bottom to top, right to left: 从下到上,从右到左遍历
for (int i = dst_image.rows - 2; i > 0; i--)
{
for (int j = dst_image.cols - 2; j >= 0 ; j--)
{
// BR
// P BR
// BR BR
std::array<cv::Point, 4> BR;
BR.at(0) = cv::Point( i - 1, j + 1 );
BR.at(1) = cv::Point( i , j + 1 );
BR.at(2) = cv::Point( i + 1, j + 1 );
BR.at(3) = cv::Point( i + 1, j );
int Fp = dst_image.at<uchar>(i, j);
//Fq
std::array<int, 4> Fq = { 0 };
Fq.at(0) = dst_image.at<uchar>(i - 1, j + 1);
Fq.at(1) = dst_image.at<uchar>(i, j + 1);
Fq.at(2) = dst_image.at<uchar>(i + 1, j + 1);
Fq.at(3) = dst_image.at<uchar>(i + 1, j);
std::array<int, 4> Dpq = { 0 };
std::array<int, 4> DpqAddFq = { 0 };
for (size_t k = 0; k < 4; k++)
{
//D(p, q)
Dpq.at(k) = D4(i, BR.at(k).x, j, BR.at(k).y);
//D(p,q) + F(q)
DpqAddFq.at(k) = Dpq.at(k) + Fq.at(k);
}
//F(p) = min[F(p), D(p,q) + F(q)]
std::sort(DpqAddFq.begin(), DpqAddFq.end());
auto min = DpqAddFq.at(0);
Fp = std::min(Fp, min);
dst_image.at<uchar>(i, j) = static_cast<uchar>(Fp);
}
}
}
int imageprocess::D4(const int& x1, const int& x2, const int& y1, const int& y2)
{
return abs(x1 - x2) + abs(y1 - y2);
}
int imageprocess::D8(const int& x1, const int& x2, const int& y1, const int& y2)
{
return cv::max(abs(x1 - x2), (y1 - y2));
}
|