摘要
简单介绍梯度的概念以及如何求解梯度,并以下山问题做比喻解释梯度下降法求解多元函数极小值的原理。接着结合下山问题与泰勒展开式等数学原理,对梯度下降法进行推导,最后给出梯度下降法的C++实现。
梯度
梯度(Gradient)在数学上为一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。在物理上可以表现为一个曲面某个点的倾斜程度、一条曲线某个点的倾斜程度。如平面函数$f$在点$(x,y)$处的梯度可以表示为
$$gradf(x,y) = \nabla f(x,y) = \frac{\partial f(x,y)}{\partial x} + \frac{\partial f(x,y)}{\partial y}$$
当自变量只有一个时,梯度可以简化为以下公式
$$\nabla f(\theta) = \frac{\partial f(\theta)}{\partial \theta}$$
多个自变量
$$\nabla f(\theta_i) = \frac{\partial f(\theta_0, \theta_1…, \theta_n)}{\partial \theta_i}$$
梯度下降法
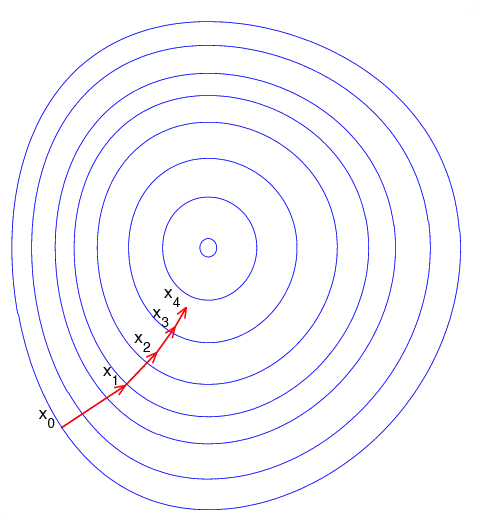
理解梯度下降法的一个简单形象的比喻就是下山问题,试想身处在山上的某个位置但没有已知的路径下山,但可以知道只要沿着位置低的方向走下去,就一定可以走下山。而且在下山问题中可以知道:每一步都沿着最陡的方向走,下山的速度就可以达到最快。而下山最陡便是梯度的变化最快,所以在求解最小函数值的时可以参考下山问题,已知函数某个点的值,要一步一步求解函数的最小值。每迭代一次就求解该点的梯度值,并且沿着梯度的负方向(下降)前进(对应自变量的更新),这样就如同下山一样可以逼近函数的最小值。
梯度下降法推导
关于梯度下降法公式推导,$文章^{【2】}$讲得非常详细。芒果这边摘取主要过程。
要推导的公式为
$$\theta = \theta_0 - \eta .\nabla f(\theta_0)$$
这是自变量的更新公式,这是梯度下降法的关键所在,用下山的比喻来说就是下山路径点的更新公式。对以上公式各个变量的解释如下:
- $\theta$: 更新后的自变量,下山问题小移动一步以后的位置
- $\theta_0$: 当前自变量,下山问题当前所在点
- $\eta$: 步长(在机器学习中又称学习速率),下山问题中下一步要走的距离长度
- $\nabla f(\theta_0)$: 当前点的梯度,下山问题中当前点陡峭的方向以及陡峭程度
推导过程
(1)直线中两点有以下关系,即求斜率
$$\frac{f(\theta) - f(\theta_0)}{\theta - \theta_0} = \nabla f(\theta_0)$$
即
$$f(\theta) = f(\theta_0) + (\theta - \theta_0) \nabla f(\theta_0)$$
(2)由微分知识可以知道,只要$(\theta - \theta_0)$两点间距足够小,曲线也可以看作直线,上式也适用,这就时一阶的泰勒展开式:
$$f(\theta) \approx f(\theta_0) + (\theta - \theta_0) \nabla f(\theta_0)$$
(3)下山的过程是每一步都希望比之前的高度低,即希望
$$f(\theta) - f(\theta_0) < 0$$
而
$$f(\theta) \approx f(\theta_0) + (\theta - \theta_0) \nabla f(\theta_0)$$
所以
$$ (\theta - \theta_0) \nabla f(\theta_0) < 0$$
又因为$(\theta - \theta_0)$是微小的矢量,梯度 $\nabla f(\theta_0)$ 也是矢量,我们知道两个矢量乘积
$$A*B = ||A||||B||cos(\alpha)$$
即令$cos(\alpha) = -1$时乘积最小,两个向量反向即可。$\nabla f(\theta_0)$方向是已知,令
$$\theta - \theta_0 = \eta.v$$
将其拆分成表示长度的标量$\eta$和表示方向的单位矢量$v$。那么只要令$v$与$\nabla f(\theta_0)$反向即可,所以
$$v = - \frac{\nabla f(\theta)}{||\nabla f(\theta)||}$$
代入上式,得
$$\theta = \theta_0 - \eta.\frac{\nabla f(\theta)}{||\nabla f(\theta)||}$$
因为$||\nabla f(\theta)||$也是标量,可以合并到长中,简化得到梯度下降公式
$$\theta = \theta_0 - \eta .\nabla f(\theta_0)$$
代码实现
这里放出芒果实现的C++版本的梯度下降法求解多元函数的极小值代码,代码也同步至GitHub,觉得对你有帮助的话不妨给个star吧。代码地址为:
https://github.com/mangosroom/machine-vision-algorithms-library/tree/master/src/base
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
//
// Created by mango on 5/08/2020.
//
#ifndef MACHINE_VISION_LIBRARY_MULTIMIN_H
#define MACHINE_VISION_LIBRARY_MULTIMIN_H
#include "opencv2/core/core.hpp"
#include <vector>
namespace mv
{
class MultiMin
{
public:
MultiMin();
~MultiMin();
virtual double Func(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters, const std::vector<double>& otherData) = 0;
bool Run(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& otherData);
//----------------------------------------设置属性 | Set property ---------------------------------------------
void SetStart(const std::vector<double>& starts);
void SetMaxtIter(const unsigned int& maxIetr);
void SetStepSize(const double& stepSize);
void SetLearningRate(const double& learningRate);
void SetConvergeThreshold(const double& convergeThreshold);
//----------------------------------------获取属性 | Get property ---------------------------------------------
std::vector<double> GetLossRecord() const { return _lossRecord; }
std::vector<double> GetResult()const { return _result; }
double GetIeterNum() const { return _iterationNum; };
private:
void CalculateGradient(const std::vector<cv::Point2d>& points, std::vector<double>& weights,
const std::vector<double>& funcParameters, const std::vector<double>& otherData, std::vector<double>& funcGradient);
//------------------------------------------输入参数 | input parameters------------------------------------
unsigned int _maxIter; // 最大迭代次数 | max iteration num
std::vector<double> _start; // 迭代起点 | iteration start points
double _stepSize; // 迭代步长 | iteration step size
double _learningRate; // 学习速率(与步长同义) | learning rate (same as step size)
double _convergeThreshold; // 收敛阈值
//------------------------------------------输出 | output---------------------------------------------------
unsigned int _iterationNum; // 运行时迭代次数 | real iteration num in runtime
bool _status; // 迭代状态 | iteration status
std::vector<double> _result;
std::vector<double> _lossRecord; // 损失值: 记录迭代收敛过程 | loss value: tracking the iteration
};
}//namespace mv
#endif //MACHINE_VISION_LIBRARY_MULTIMIN_H
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
|
//
// Created by mango on 5/08/2020.
//
#include"multimin.h"
#include<iostream>
using namespace mv;
MultiMin::MultiMin()
{
// 参数默认值
_maxIter = 100;
_learningRate = _stepSize = 0.001;
_convergeThreshold = 1e-10;
_status = false;
}
MultiMin::~MultiMin()
{
}
void MultiMin::SetStart(const std::vector<double>& starts)
{
_start = starts;
}
void MultiMin::SetMaxtIter(const unsigned int& maxIetr)
{
_maxIter = maxIetr;
}
void MultiMin::SetStepSize(const double& stepSize)
{
_stepSize = stepSize;
_learningRate = stepSize;
}
void MultiMin::SetLearningRate(const double& learningRate)
{
_learningRate = learningRate;
_stepSize = learningRate;
}
void MultiMin::SetConvergeThreshold(const double& convergeThreshold)
{
_convergeThreshold = convergeThreshold;
}
void MultiMin::CalculateGradient(const std::vector<cv::Point2d>& points, std::vector<double>& weights,
const std::vector<double>& funcParameters, const std::vector<double>& otherData, std::vector<double>& funcGradient)
{
funcGradient.clear();
double h = _stepSize;
double gradient = 0;
std::vector<double> fhv = funcParameters;
for (size_t i = 0; i < funcParameters.size(); i++)
{
fhv.at(i) += h;
double f = Func(points, weights, funcParameters, otherData);
double fh = Func(points, weights, fhv, otherData);
// 第i个函数变量方向的梯度
gradient = (fh - f) / h;
funcGradient.push_back(gradient);
}
}
//
bool MultiMin::Run(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& otherData)
{
// 迭代起始位置
std::vector<double> iterVale = _start;
std::vector<double> gradient(iterVale.size(), 0);
double funcValue = 0; //当前函数值
double lastFuncValue = 1e9; //上一次函数值
int stayConvergeTimes = 0; //驻留收敛次数
// 清空收敛记录
_lossRecord.clear();
// 开始迭代
_iterationNum = 0;
for (size_t i = 0; i < _maxIter; i++)
{
_iterationNum++;
// 计算梯度
CalculateGradient(points, weights, iterVale, otherData, gradient);
// 梯度下降公式迭代修正
for (size_t j = 0; j < iterVale.size(); j++)
{
iterVale.at(j) -= _stepSize * gradient.at(j);
}
// 重新计算当前函数值
funcValue = Func(points, weights, iterVale, otherData);
double difference = std::abs(funcValue - lastFuncValue);
if (difference < _convergeThreshold)
{
stayConvergeTimes++;
}
else
{
stayConvergeTimes = 0;
}
_lossRecord.push_back(funcValue);
lastFuncValue = funcValue;
if (stayConvergeTimes > 10)
{
_result = iterVale;
_status = true;
return _status;
}
}
//std::cout << iterVale.at(0) << " " << iterVale.at(1) << std::endl;
_result = iterVale;
_status = false;
return _status;
}
|
使用方法为继承该类,并实现自己定义的损失函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
class MultiminTest: public MultiMin
{
public:
MultiminTest();
~MultiminTest();
double Func(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters, const std::vector<double>& otherData) override;
private:
double HuberLoss(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters, const double& outlierThreshold);
double MAELoss(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters);
FitAlgorithms _fitAlgorithms;
};
double MultiminTest::MAELoss(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters)
{
int N = static_cast<int>(points.size());
double a = funcParameters.at(0);
double b = funcParameters.at(1);
//MAELoss
double sum = 0;
for (int i = 0; i < N; i++)
{
double yi = points.at(i).y;
double fi = a * points.at(i).x + b;
double dist = std::abs(yi - fi);
sum += dist;
}
return sum / N;
}//MAELoss
double MultiminTest::HuberLoss(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters, const double& outlierThreshold)
{
int N = static_cast<int>(points.size());
double a = funcParameters.at(0);
double b = funcParameters.at(1);
double sum = 0;
for (int i = 0; i < N; i++)
{
double yi = points.at(i).y;
double fi = a * points.at(i).x + b;
double dist = std::abs(yi - fi);
// huber loss
if (dist <= outlierThreshold)
{
// 更新权重
weights.at(i) = 1;
dist = 0.5 * dist * dist;
}
else
{
// 更新权重
weights.at(i) = outlierThreshold / std::abs(dist);
dist = outlierThreshold * dist - 0.5 * outlierThreshold * outlierThreshold;
//dist *= weights.at(i);
}
sum += std::abs(dist);
}
return sum / N;
}//HuberLoss
double MultiminTest::Func(const std::vector<cv::Point2d>& points, std::vector<double>& weights, const std::vector<double>& funcParameters, const std::vector<double>& otherData)
{
double outlierThreshold = otherData.at(0);
double sum = 0;
switch (_fitAlgorithms)
{
case FitAlgorithms::REGRESSION:
break;
case FitAlgorithms::HUBER:
sum = HuberLoss(points, weights, funcParameters, outlierThreshold);
break;
case FitAlgorithms::TUKEY:
break;
case FitAlgorithms::DROP:
break;
case FitAlgorithms::GAUSS:
break;
default:
break;
}
return sum;
}
|
References
【1】梯度下降法-维基百科
【2】简单的梯度下降算法,你真的懂了吗?-AI有道
【3】梯度下降(Gradient Descent)小结-刘建平Pinard
本文由芒果浩明发布,转载请注明出处。
本文链接:https://blog.mangoeffect.net/algorithm/deduce-and-achieve-gradient-descent.html


